- ...
matrices,2.1
- Note that the corresponding Boolean algebra for
these matrices is a semiring where
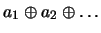 because as
mentioned above, in a Boolean semiring, the additive operator
because as
mentioned above, in a Boolean semiring, the additive operator
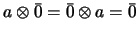 corresponds to OR.
corresponds to OR.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...,2.2
-
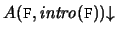 means defined.
means defined.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... chart:7.1
- Note that
for ease of exposition, we are showing a simplified version of the
code here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... below:8.1
- VF stands for Vorfeld, CF for
Complementiser Field (left sentence-bracket), MF for Mittelfeld, VC
for Verbal Complex (right sentence-bracket), and NF for Nachfeld
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Prolog.10.1
- The above information has been adapted from
http://wombat.doc.ic.ac.uk.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.